大家好,我是电源漫谈,很高兴和各位一起分享我的第7篇原创文章,喜欢和支持我的工程师,一定记得给我点赞、收藏、分享。
加微信[13764329639]与作者微信及进群沟通交流。
以前,我们讨论过测试DC/DC电源的小信号环路特性的方法,但是没有讲清楚如何去判断环路的稳定性,所以,我们通过本文系统讲述一下如何判断电源系统的环路稳定性及相关的一些背景知识。
一.环路控制的必要性
这里还是以BUCK电路为例进行讨论,当一个BUCK电路未进行闭环控制的时候,如图1所示。
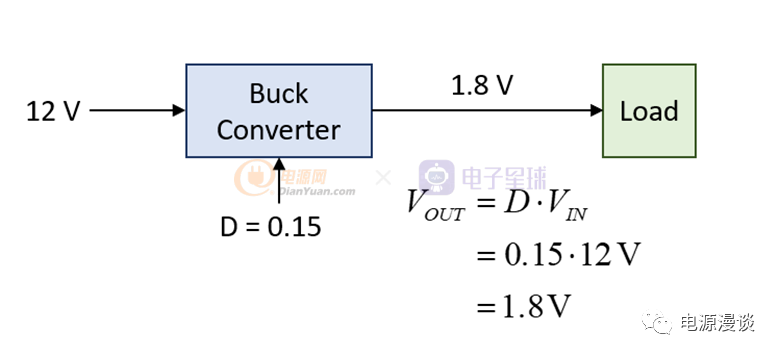
图1 未进行环路控制的BUCK电路
定义这里蓝色框内的仅仅是一个BUCK电路的功率级,我们给一个固定的占空比0.15驱动BUCK电路上管,根据其基本工作原理,输出电压为12V*0.15=1.8V,当输入电压或者输出电流改变时,那么,由于未对输出进行控制,所以输出电压一定会变化,如输入电压变为9V时,则输出电压变为1.35V,这明显是不满足应用的需求的。所以,一定需要一个闭环控制回路,来保持输出电压不随着输入电压或者负载电流变化而变化,即保持恒定。
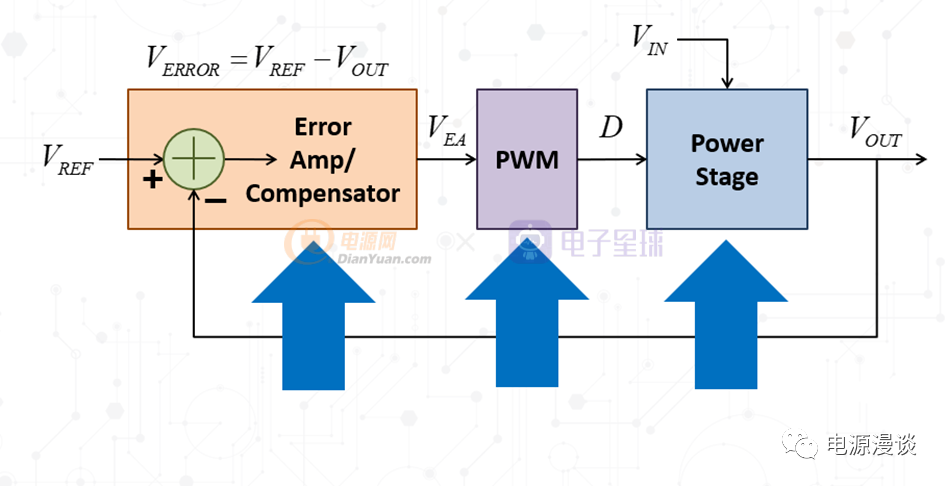
图2 施加了闭环控制回路后的电源原理框图
当我们添加了控制回路后,它对输出电压进行采样监控(这里我们忽略反馈分压比例环节,或者将它看作补偿器中的部分),采样结果和参考电压相比较,产生误差,通过误差去对PWM占空比控制,从而保持输出电压的恒定,它就具有了一般的闭环控制功能。
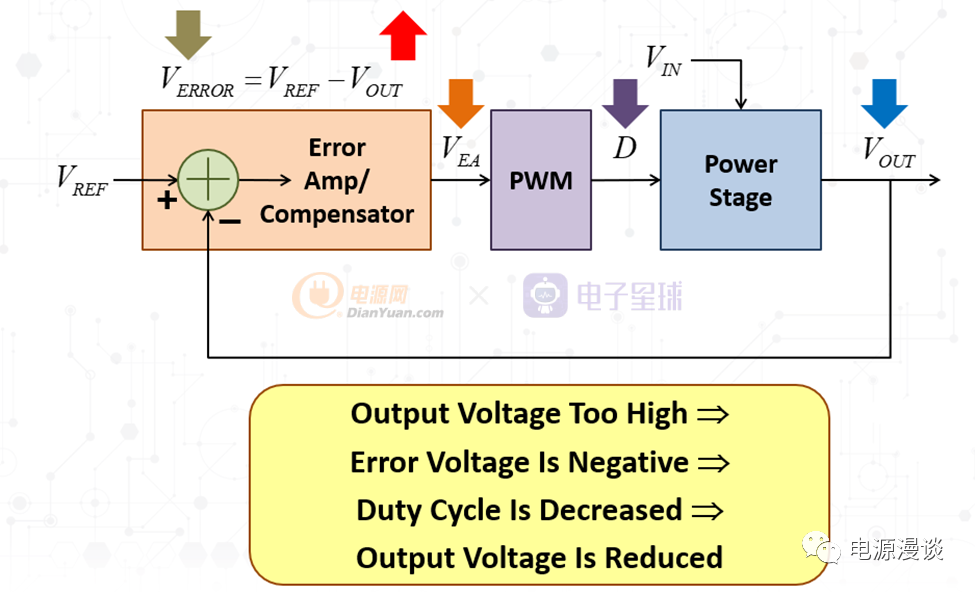
图3 输出电压增加时的反馈调节过程
当输出电压由于某种原因,增加时,如图3所示,则通过和参考电压VREF相减,误差会减小,所以输入给PWM调整器后,输出占空比会减小,从而让输出电压减小。值得注意的是,从输出电压变大到占空比得到调整,以及最终输出电容和电感上的能量重新调整,从而保持输出电压回到原来的设定值,需要一定的时间。
输出电压减小时的情况和上述输出电压增加时类似,我们不做太多讨论,想必大家也清楚了。
二.在复平面上分析传递函数的性能
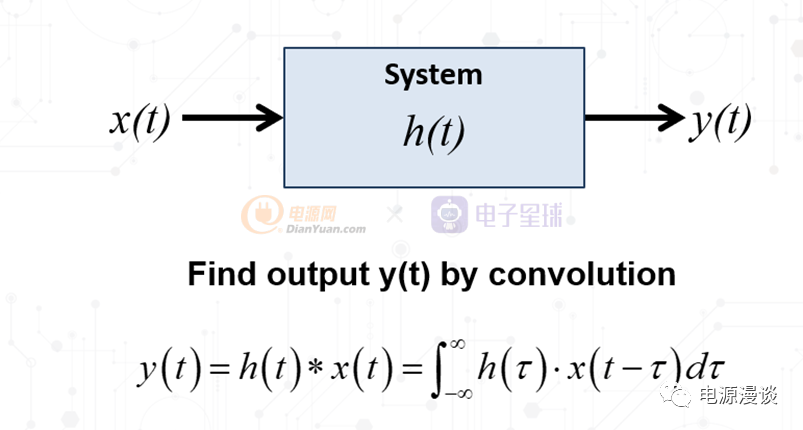
图4 线性系统时域传输关系
当我们给一个线性系统输入一个时域函数时,由于系统的输入到输出的时域传输关系是固定的,所以一定会得到一个相应的时域输出函数。由于电源系统中,靠开关的高速动作,电源系统是一个非线性系统,但是我们仍旧可以把一个在稳定工作的电源的工作点的附近区域看作一个线性系统,所以可以用线性系统的原理去分析它。
我们回顾一些旧的知识,我们知道,任何周期性波形信号,都可以看成是一组离散频率的正弦波信号组成的,这些频率都是基波频率的整数倍,将一个周期性信号分解为一组离散频率信号的分析方法就是傅里叶分解。
那么,类似地,分析任意波形的信号在一个线性系统上的响应时,我们可以将任意波形分解为一组连续频率的信号的组合,以此分析输入信号在线性系统上的响应,这就是频域分析。
电路中如果含有电感,或者电容等等器件,则随着时间变化,一个激励信号产生的响应是随时间变化的,电压和电流之间会有相位差,所以,对这样的系统进行时域分析时,不能用算术分析法,而只能用矢量分析法。
各种元器件阻抗都可以在时域中用都可以用矢量表示,电压和电流也都可以用矢量表示,只要给出实部和虚部,都可以求出矢量的模和幅角,对应矢量的幅值和相位这两个量。
在时域分析中,可以用
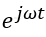
来表示正弦波激励,去求解线性系统的稳态输出响应,但是计算相对复杂,所以我们引入了复平面,即s平面,在s平面上做线性系统的稳态分析,
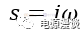
,而所有元件在s平面上都可以表示为相应的形式,此时我们可以将s平面上的系统的输入输出关系表达求出来,我们称作s域传递函数。
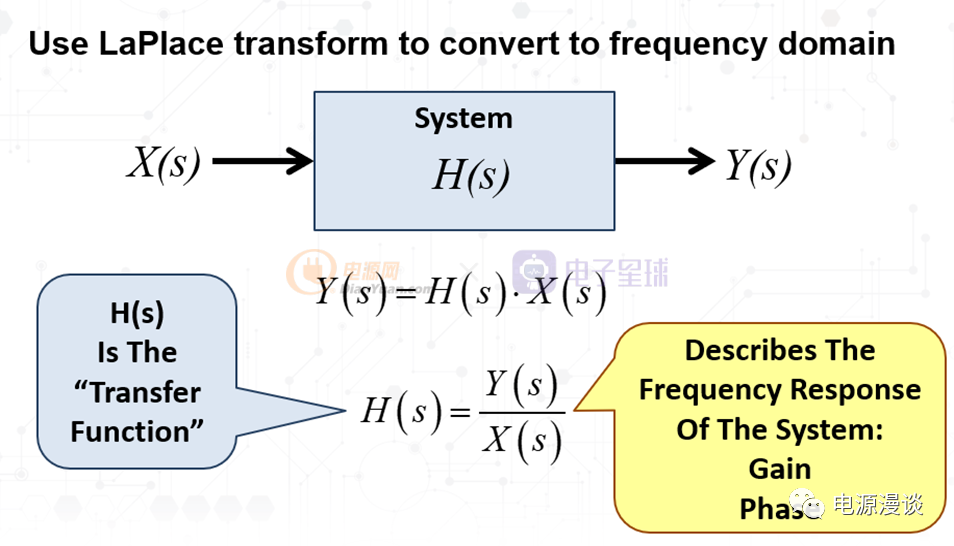
图5 s域传递函数的表达形式
将我们分析的系统用传递函数表达后,可以得到一个s域表达式如图5所示,,只要给出一个输入激励,就可以求得输出响应,此响应包含输出信号的相位和幅值信息。
三.通过开环传递函数评估闭环性能
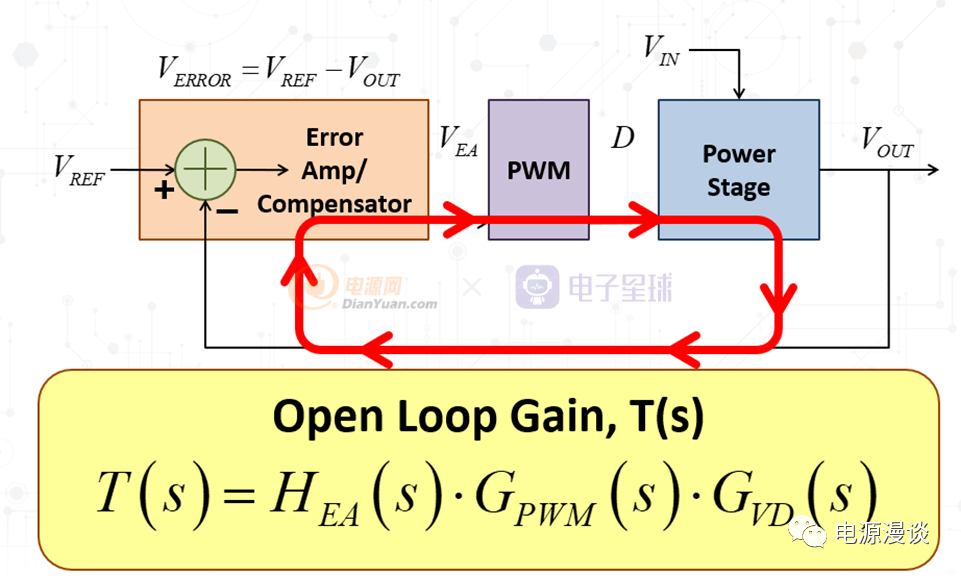
图6 电源系统开环传递函数
到复平面上后,我们将组成闭环系统的每一个环节都变换为S域的传递函数,那么整个系统的传递函数,就是各个环节的乘积,如图6中的T(s),包含反馈补偿器部分HEA(s),PWM调制器环节GPWM(s),功率级环节GVD(s)等,这个T(s)包含了信号在整个环节走一圈,所产生的响应的幅值和相位变化信息。
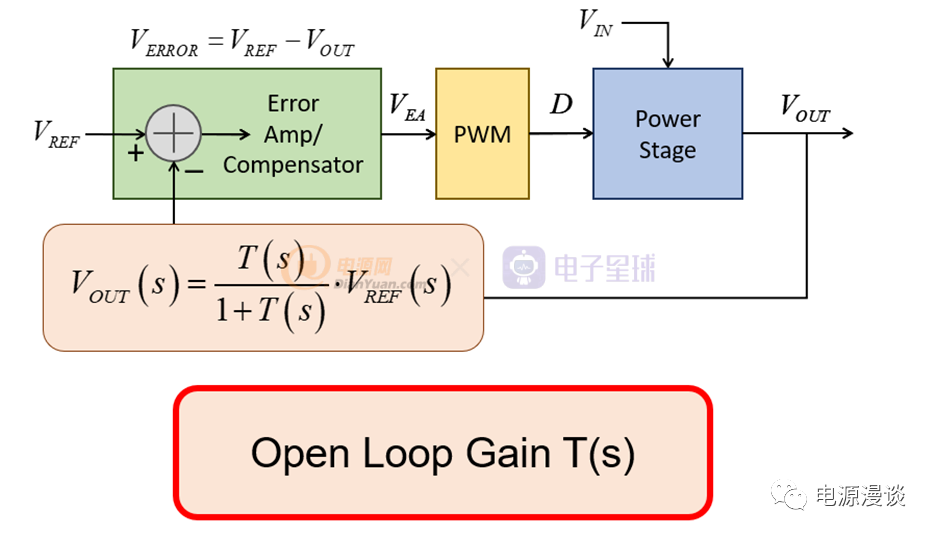
图7 开环增益传递函数T(s)和闭环传递函数的关系
我们可以根据上述反馈系统的结构,求得闭环传递函数(此处不做推导关系的解释),也就是VREF到VOUT的传递函数,如上述图7的表达式。分析一下这个表达式,有两个关键信息,其一,当T(s)为无穷大的值时,输出的响应Vout(s)必然等于输入信号VREF(s),所以提高开环传递函数的增益,对输出调整性能的精确性非常有帮助。
其二,当分母为0时,也就是T(s)+1=0时,输出响应Vout(s)为无穷大,从输入端给定一个输入信号后,输出变为一个不可控的值,这显然是不稳定的反馈系统。
接下来我们重点分析一下T(s)为-1这个不稳定点,如何避免这个不稳定点的发生。
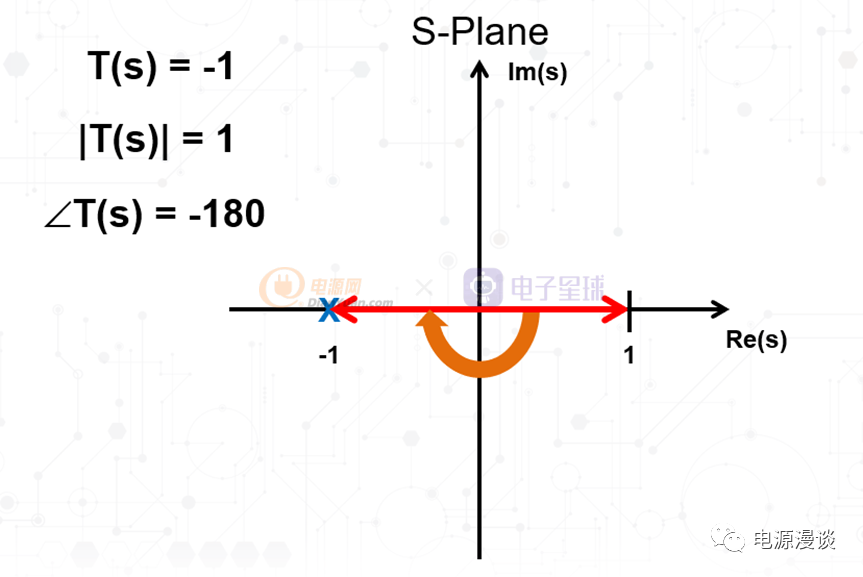
图8 T(s)在s平面上的不稳定点
在s平面上,因为这是复数平面,所以当T(s)为-1时,意味着T(s)=-1+j*0,通过计算,这个矢量的模为1,幅角为-180C,即由下式得出。
所以根据以上计算结果,为了让系统不进入不稳定点,则需要不能让这两个条件都满足,即当增益为1时(对数纵坐标中是0db),相位变化不能达到-180C或者180C(一般为滞后相位-180C),而当相位达到-180C时,增益不是0db,而是有一个衰减。
如果一个扰动量,经过开环传递函数一周回到注入点后,发现相位不变,幅值也不变,则说明这个系统一定是不稳定的,因为考虑负反馈已有的180C相移外,系统又带来了180C的相移才保持相位不变,因此其没有相位裕量。
四.相位裕量和穿越频率的变化分析
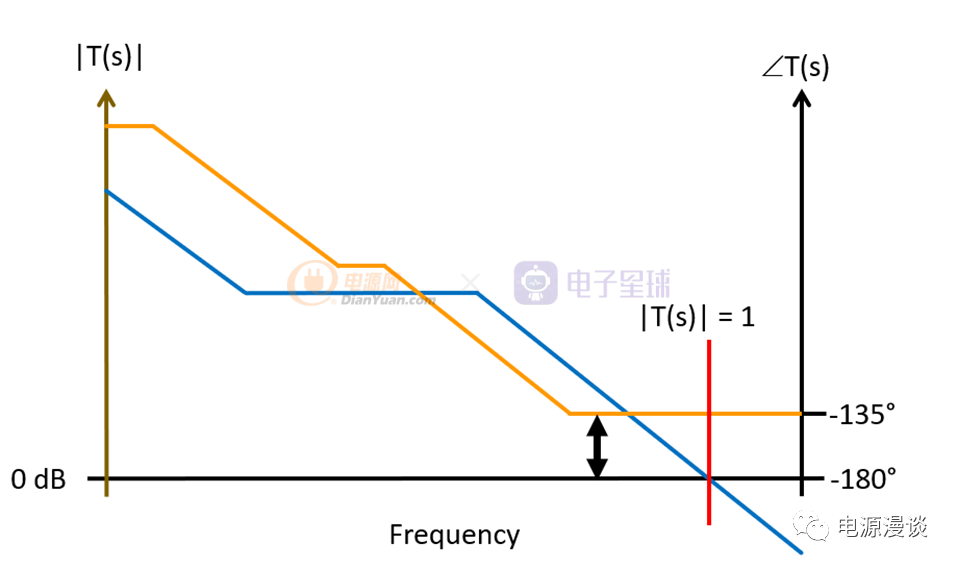
图9 典型相位裕量
上述我们通过开环增益传递函数性能分析了闭环不稳定条件,需要保持一个足够的相位裕量,图9给出了一个典型的相位裕量,45C(180C-135C),其概念就是当增益为0db时,也就是T(s)的模为1时,其相位变化相距-180C还有45C,所以认为它是相对为稳定的,这样就确保在电路参数一定的精度容差下,及温度变化导致器件参数变化的情况下,随着时间器件老化的情况下,系统都能离不稳定点有一定距离,我们称做具有45C相位裕量。
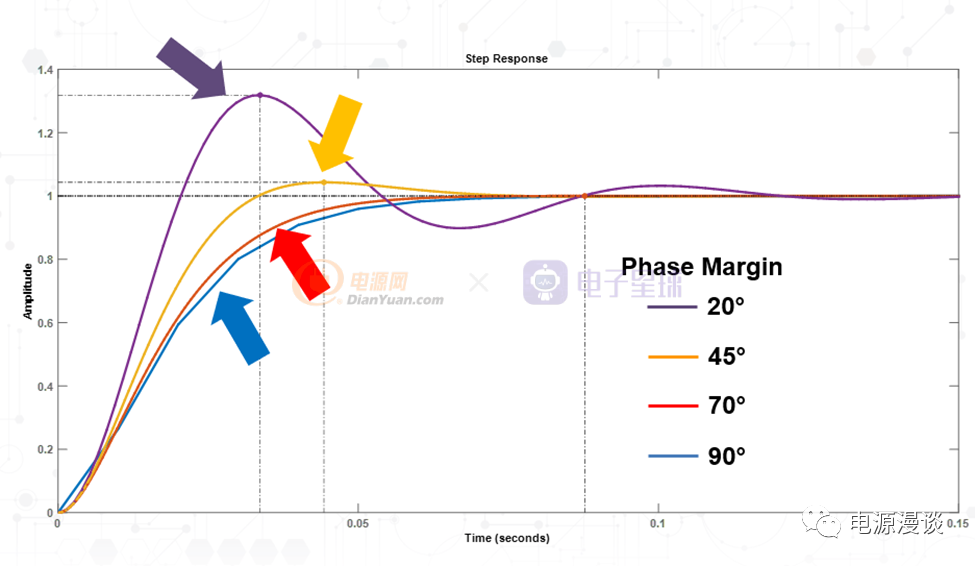
图10 不同相位裕量和阶跃响应的关系
除了45C,在其它相位裕度的情况下,系统的稳定性如何呢?图10给出了展示,可以看出当相位小于45C时,系统在阶跃响应时会发生比较多的震荡,而在45C以上时系统是相当稳定的,这说明在阶跃响应下,系统的输出过冲非常小。
除了相位裕量这个指标,还有一个参数对于系统响应非常重要,就是T(s)达到0db时的频率,当这个频率越大时,系统响应速度越快,因为在增益曲线上更高的频率的误差信号将得到放大,进而控制闭环响应。
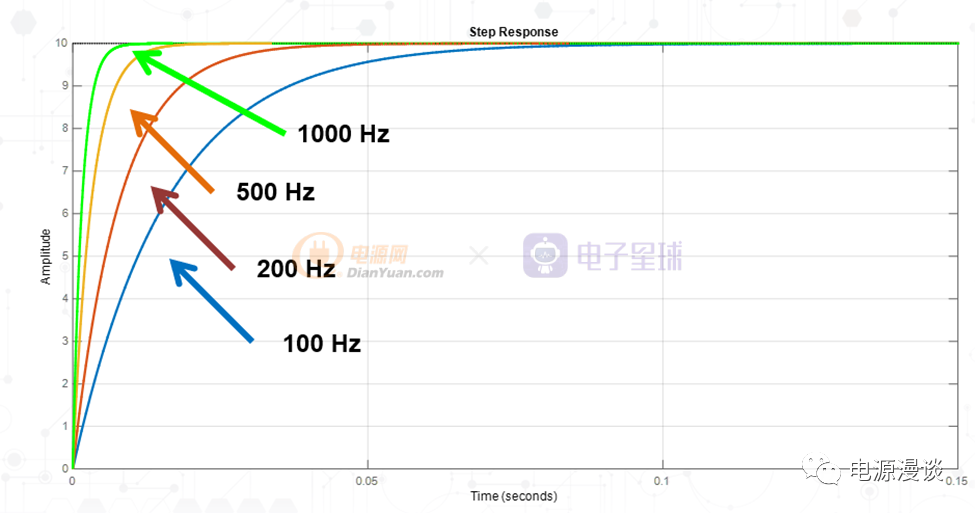
图11 不同穿越频率下的阶跃响应
图11给出了不同穿越频率下的阶跃响应,当穿越频率高时,举例来说,图示1k时,系统输出很快就得到了调整,而穿越频率低时,例如100Hz,需要等待较长时间才慢慢调整好。所以一般设计会保持较大的穿越频率,以便让系统得到快速响应,但是也要注意,穿越频率应该小于任何不稳定频率,比如右半平面零点(Boost类的拓扑),或者峰值电流模式次谐波震荡频率点(一半开关频率)等,以及在数字控制中需要小于奈奎斯特频率(开关频率的一半,如每周期都采样的话)等。
一般情况下,对于模拟控制电源,建议穿越频率设置为1/10的开关频率,数字控制设置在1/20的开关频率。

图12 环路稳定性判据
所以,综上所述,一般建议环路设计参数如图12所示。
五.一些特殊的情况分析
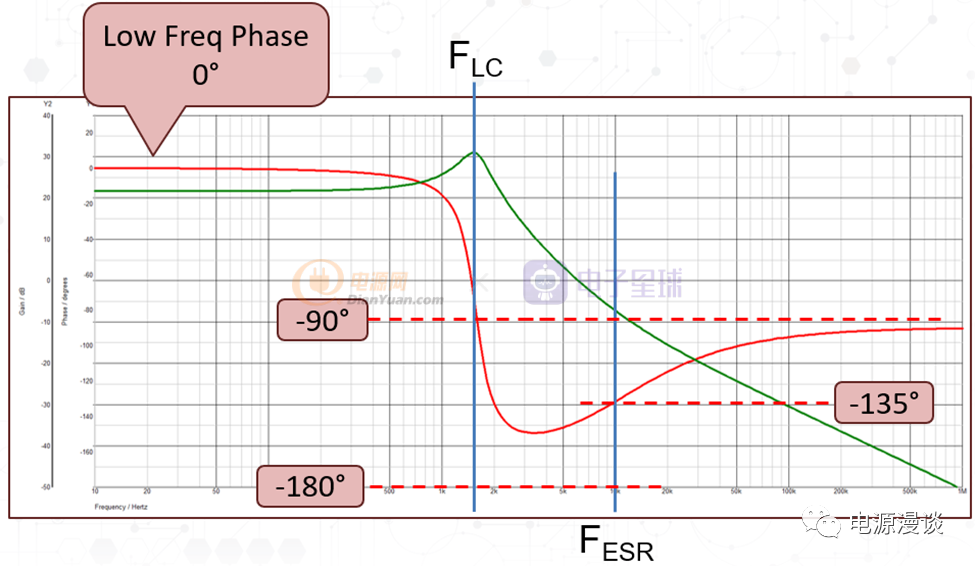
图13 二阶系统的双极点Q值影响
在典型的二阶系统功率级电路中,由于电感和电容元件参数或者负载状态,导致极大的Q值,那么很可能在转折频率处直接产生180C的相位快速下掉,而不是在转折频率处先产生90C相位下掉然后再逐步下掉到-180C,这时候很可能产生这些频率附近的不稳定现象,在设计中需要注意。
一个典型的性能良好的反馈系统,除了具有小信号稳定性之外,对一些大范围的阶跃响应,或者极限输入,极限输出条件下,也要保持大信号稳定性。例如,在大负载阶跃激励时,输出的响应过冲电压取决于输出电容的供电能力,此时输出电容需要确保将输出电压稳定在一定范围内,之后控制环路起作用将输出调回到原始设定状态。
总结,上述详细讨论了环路控制的必要性,环路稳定性评估的分析,影响系统相对稳定性的不同参数的影响,及一些特殊情况的考虑,通过本文可以对环路控制稳定性评估有一定的理解。

