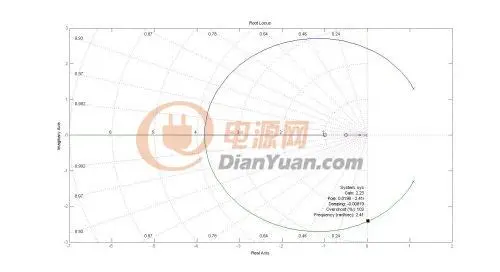
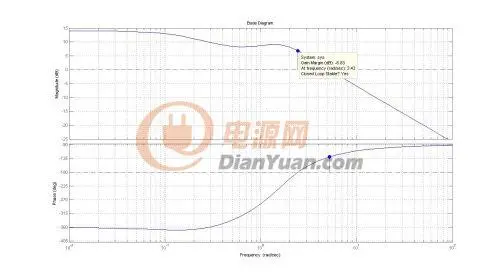
系统稳定性判断

这图是前后两页。

出自：（自动控制理论第3版  邹伯敏 ）P249  P250页

你把书上的这个结论：增益越低，稳定性越好，再截个图传上来~

我想看看哪本书会有如此绝对的结论~

bode兄，我将书上的话 单独截出来了。书上原话说的就是：增益越小， 时常越大，系统稳定性就越好。

说明：Ti：时间常数

            Kp：系统增益

首先，开环增益越低，系统稳定性越好，这句话是有应用前提的，它是针对一个系统的总增益曲线而言的。但我们有时候讨论的时候，是省略了这个前提，很容易造成误解~

对于一个稳定的系统，增益曲线要以-20/dec衰减穿越截止频率，相应的相频曲线，也要以-45度/dec衰减，趋向-180度线。这是一个典型稳定系统的bode图特征。

如果一个系统增益曲线以-20/dec衰减穿越截止频率，而相频曲线是45度/dec递增，那么这个系统的校正环路肯定是不合适的，这样使得高频特性很差。

PI调节器只是作为一个完整系统的一部分，即控制环节，它的这个特点，并不足以否定  开环增益越低，系统稳定性越好 这个观点。

另外，开环增益越低，系统稳定性越好 这个观点，也并不是绝对的。

书上常说的话，应该是这样的：过大的开环增益，可能会使系统振荡，但并不意味着 开环增益越小越稳定。

如果用比例积分环节作为一个控制器，去调控一个控制对象的话，

比例K越大，系统稳定性越差；

积分时间常数越小，积分控制作用越强，但系统稳定性越差~

另外，开环增益越低，系统稳定性越好 这个观点，也并不是绝对的。

请bode兄，举个例子说明。

看看这个根轨迹图，只有当根轨迹增益达到一定值时，开环极点才会运动到右半平面~

可以的，开环传递函数是这样的~

俺得寸进尺，请兄将这个传递函数的bode图 给出来 。matlab就是干这事的吧。matlab你的强项，呵呵

就拿纯积分环节来说

G=K/S；

无论K怎么变化，相位裕度都是90度，不发生变化~

千万别这么说，大家通过讨论，共同进步~

哈哈，这个例子好，它说明了：

1。增大增益，相位裕度减少，系统稳定性变差

2。减小增益，相位裕度增大，系统稳定性变好

这两句话，如果绝对地来理解都是错的。

上面两句话的正确性，要看具体的情况，是这样的吧。

我在第7贴，已经答复过了~

开环增益的提高或者降低的影响，都是针对系统级里说的，对于单个的环节，比如控制环节、被控对象来说，是不适用的~

当然，对于最小相位系统来说，开环增益越低，系统越稳定，这句话在大多数情况是成立的~