图解傅里叶变换

首先回顾一下傅里叶变换

以方波为例，近似认为任何波形都可由不同频率、幅值和相位的正弦波组合而成，傅里叶变换就是将任意波形（这里的方波）中的各分量分离出来。如何分离？硬件上可以采用窄带滤波器，但实际上硬件开销是难以接受的，通常采用的是数学方法——欧拉滤波器。

欧拉公式

欧拉公式展示了一根螺旋上升的曲线（如同弹簧），这根神奇的“弹簧”或许更加接近事物的本质，我们通常所能观察到的或许只是这个三维模型的某个投影。

这里就是借用这个三维欧拉模型来分离频域中的各个分量实现滤波效果。

设一个频率为f0=0.3Hz正弦波信号其时域、频域图如下：

                                              图1-1  0.3Hz正弦波时域、频域图

如图把时域信号乘以欧拉公式再积分取模就得到了频域信号，这一步又称卷积。这时脑袋里就产生了问号，啥是卷积？为啥欧拉公式能滤波？复数怎么算？渣一样的数学水平是不可能理解这个方程了，那么就换一个角度看看能不能把这个方程的轨迹描绘出来，通过过程说不定就能够理解这个方程的机理。

一个时域信号乘以欧拉公式后是怎么的轨迹？取欧拉公式中的频率也为f0=0.3Hz，复平面图形如下：

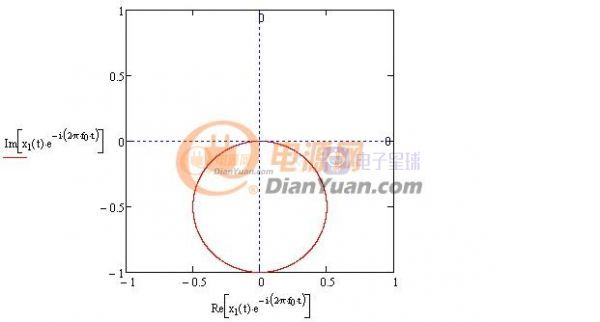
                                         图1-2  f0=0.3Hz复平面图

在三维模型中的轨迹如下：

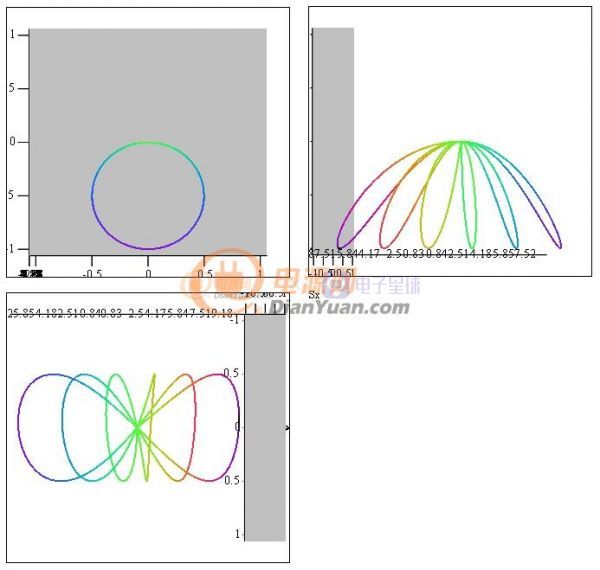
                                               图1-3 三视图

三视图中灰色的是XY平面（复平面），实际发现Z轴（时间轴）上的数值对结果没有影响，只需关心在XY平面的投影即可。从这里看似乎复平面二维图就足够了。

  接着用欧拉滤波器进行扫频观察复平面、三维图中轨迹的变化：

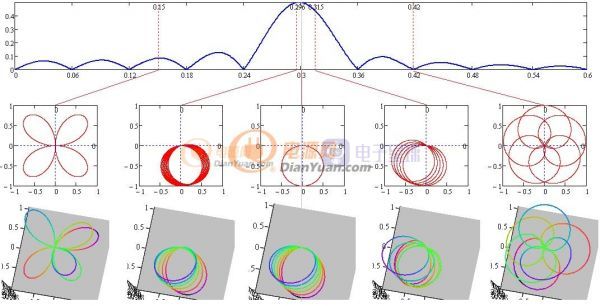
                                      图1-4 对比频域中各频率对应的复平面和三维图

  通过观察发现所有轨迹在复平面的投影重合度越高的对应的频域值越大，比如欧拉滤波器取f0=3Hz时所有轨迹的投影在一个圆上，而偏离f0=3Hz时投影逐渐散开（如同弯曲的弹簧），在f0=0.42Hz处所有投影成对称状（复平面有正有负）得到的频域值为零。

  再观察最左边的f0=0.15Hz处，放大如下：

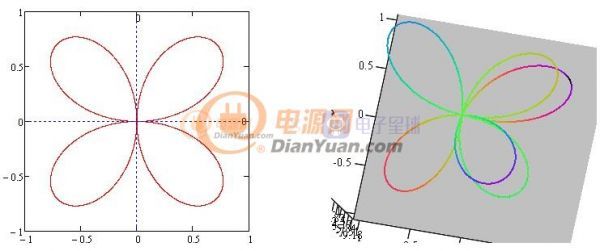
                                                  图1-4-1 f=0.15Hz放大图

在复平面中其为对称图形得出的频域值应该为零但实际不为零，通过观察三维图右边的两个臂为双重臂所以单纯在二维投影中分辨不出来。那么怎样来求这些投影的重合度？

因为复平面中有正有负当把所有点相加后对称的部分会抵消掉这样就能判断出重合度（或应称对称性），再取模就得出了实数结果。对乘积项进行累加（积分）也就是卷积运算了，卷积运算比较慢有没有其它更便捷的方法来识别投影的重合度（对称性）？或者优于欧拉滤波器的滤波器？

如果不是单一频率的波形仍然符合上述规律只是投影不再是标准的圆形，见下图：

                                        图1-5 两种频率的合成波频域及投影

再来分析相位的识别方法，观察下面不同初始相位时对应的X方向Y方向上投影：

                                               图1-6-1 0度对应的投影

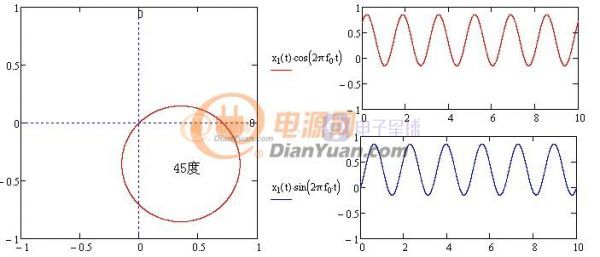
                                                 图1-6-2 45度对应的投影

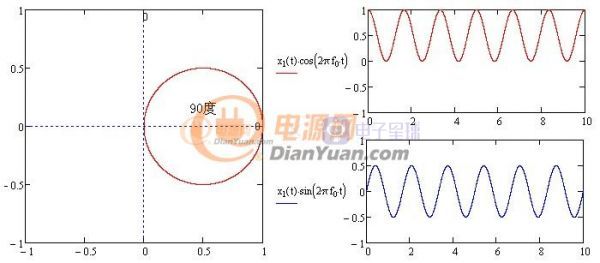
                                                   图1-6-3 90度对应的投影

通过对比可知初始相位可以用图中两条正弦波的均值求反正切获得，这两条正弦波为原波形x1(t)分别与欧拉公式的虚部、实部相乘获得（欧拉三角形式cos(t)-i*sin(t)），平均值可由积分的方法获得，最终求相位也用到了卷积，表达式及波形如下：

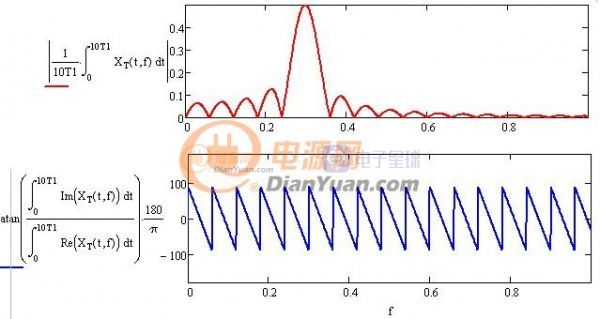
                                                         图1-7 频率相位图

（此处有点小问题，结果相差90度）

傅里叶级数、傅里叶变换、DFS、DTFT

根据信号的不同类型，可以把傅立叶变换分为四类：

1) 非周期性连续信号： 傅立叶变换(Fourier Transform，FT)

2) 周期性连续信号： 傅立叶级数(Fourier Series，FS)

3) 非周期性离散信号： 离散时域傅立叶变换(Discrete Time Fourier Transform ,DTFT)

4)周期性离散信号： 离散傅立叶变换(Discrete Fourier Series，DFS)

前面分析的都是周期信号特点时域连续周期，对应频域离散非周期属于傅里叶级数

                                              图2-1 傅里叶级数

对于非周期信号特点时域连续非周期，对应频域连续非周期属于傅里叶变换

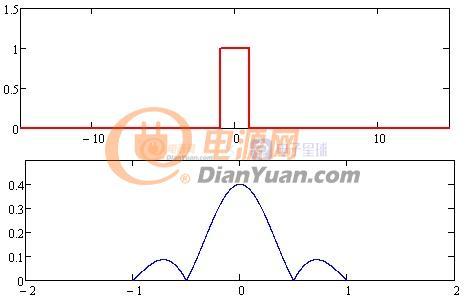
                                                 图2-2 傅里叶变换

傅里叶变换变换某种程度上可以看做傅里叶级数在单个峰上的拉伸，虽然y轴值有所不同但频域反映的是比重似乎影响不大。

前面提到卷积的运算速度比较慢，采用离散化处理后可以减少运算次数提高运算速度，再者现在的计算机都是数字计算机对于连续的模拟数据只能抽样处理。

拉普拉斯变换

在实际波形中会出现不收敛的曲线，这种曲线的轨迹示意如下：

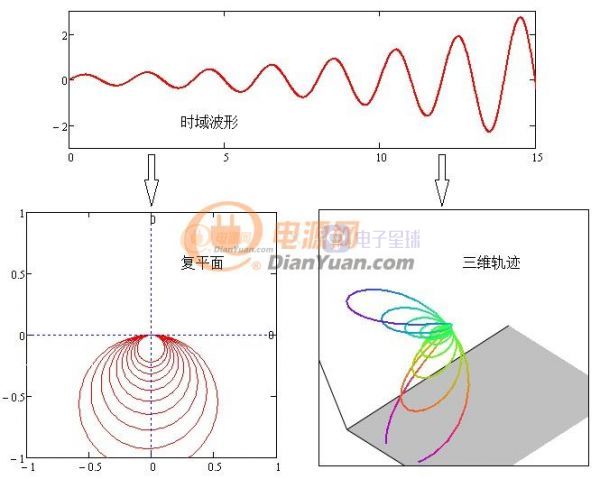
                                                       图3-1 发散曲线

从三维图看沿时间轴方向螺旋半径越来越大导致积分结果无穷大既不可积，这样就没办法用之前的方法来鉴别频率了。拉普拉斯先生对此做了改进加入了衰减函数——e^-σt其中σ为正实数，为什么用e指数？有资料说e指数曲线是自然界衰减最快的曲线。加入这个衰减函数后的效果如何呢？

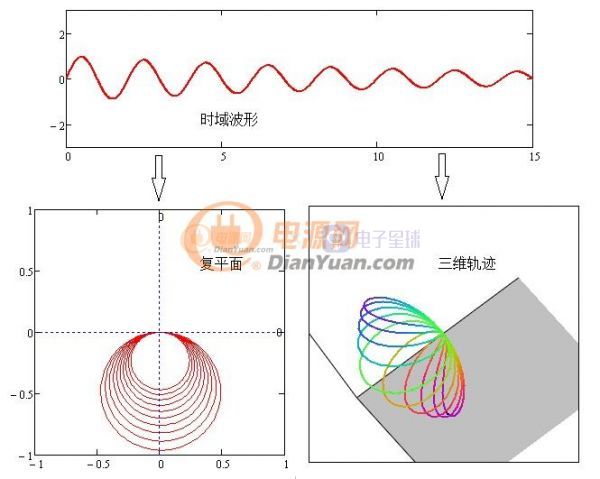
                                                    图3-2 收敛曲线

这里可以通过调系数σ来调衰减程度，虽然衰减函数加在傅里叶公式上，通过公式变换或者实际效果看跟加在时域波形上的效果一样，换句话说先对时域波形进行收敛处理后再做傅里叶变换等同于拉普拉斯变换。

拉普拉斯变换公式：

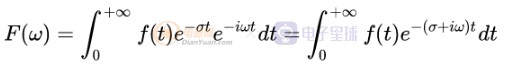
                                                      图3-3 欧拉滤波器VS拉普拉斯滤波器